dropping variables from multilinear model test|when to drop variables in multiple linear regression : purchasers Use the leaps library. When you plot the variables the y-axis shows R^2 adjusted. You look at where the boxes are black at the highest R^2. This will show the variables you should use for your multiple linear regression. Wine . WEB27 de jan. de 2023 · Fotos do ex-ator pornô Kid Bengala aparecem em perfil de Luan Santana no Twitter. Cantor teve sua conta, que soma mais de 11,7 milhões de .
{plog:ftitle_list}
Sinopse. Un homme à la capacité mentale d'un enfant de 10 ans peut-il devenir un chirurgien pédiatrique brillant? Park Si On (Joo Won) est un jeune homme avec le .
when to drop variables in multiple linear regression
sony xz premium drop test
multiple linear regression models examples
If I given a model with 3 variables($X_1, X_2$ and $ X_3$) and a correlation between them are not high. The highest correlation coefficient from the correlation matrix is .Use the leaps library. When you plot the variables the y-axis shows R^2 adjusted. You look at where the boxes are black at the highest R^2. This will show the variables you should use for your multiple linear regression. Wine . How do we detect and remove it? So let’s begin answering these questions one by one. 1. What is multicollinearity? Multicollinearity is a condition when there is a significant .
Multicollinearity using Variable Inflation Factor (VIF), set to a default threshold of 5.0; You just need to pass the dataframe, containing just those columns on which you want to . Most common method for dealing with missing values when we have more than 80% missing data is to drop and not include that particular variable to the model. So, we will . Multicollinearity occurs when your model includes multiple factors that are correlated not just to your target variable, but also to each other. Now let’s explain this in .
Dividing the test data into X and Y, after that, we’ll drop the unnecessary variables from the test data based on our model. Now, we have to see if the final predicted . Introduction. Multicollinearity, a common issue in regression analysis, occurs when predictor variables are highly correlated. This article navigates through the intricacies of .
sony xz1 drop test
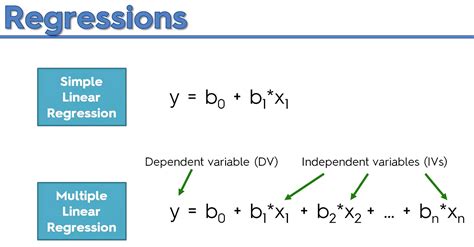
Multicollinearity occurs when two or more independent variables are highly correlated with one another in a regression model. How can we detect multicollinearity in our . Multilinear regression is a statistical method used to model the relationship between a dependent variable and multiple independent variables. It is an extension of simple linear regression and allows for the analysis of more complex relationships between variables. What is a "p-value" in multilinear regression? Here, Y is the output variable, and X terms are the corresponding input variables. Notice that this equation is just an extension of Simple Linear Regression, and each predictor has a corresponding slope coefficient (β).The .This repository contains a Jupyter Notebook that demonstrates how to perform multiple linear regression using the scikit-learn library in Python. The notebook includes detailed steps for data exploration, model fitting, visualization, and .

A group of \(q\) variables is multilinear if these variables “contain less information” than \(q\) independent variables. Pairwise correlations may not reveal multilinear variables. The Variance Inflation Factor (VIF) measures how predictable it is given the other variables, a proxy for how necessary a variable is: I want to run a linear regression model with a large number of variables and I want an R function to iterate on good combinations of these variables and give me the best combination. The multiple regression model is: The details of the test are not shown here, but note in the table above that in this model, the regression coefficient associated with the interaction term, b 3, is statistically significant (i.e., H 0: b 3 = 0 versus H 1: b 3 ≠ 0). The fact that this is statistically significant indicates that the association between treatment and outcome .
A regression model is a statistical model that estimates the relationship between one dependent variable and one or more independent variables using a line (or a plane in the case of two or more independent variables). A regression model can be used when the dependent variable is quantitative, except in the case of logistic regression, where .
One of the main questions you’ll have after fitting a multiple linear regression model is: Which variables are significant?. There are two methods you should not use to determine variable significance:. 1. The value of the regression coefficients. A regression coefficient for a given predictor variable tells you the average change in the response variable .
Yes, drop the statistically insignificant dummy variables and re-run the regression to obtain new regression estimates. The dummy variables that are statistically insignificant are no different from the category that was omitted in the n-1 choice, For example, in the example discusses above, the fact that “Married” and “Divorced” have insignificant coefficients means .
group of predictors are in the model. • In CHS example, we may want to know if age, height and sex are important predictors given weight is in the model when predicting blood pressure. • We may want to know if additional powers of some predictor are important in the model given the linear term is already in the model.
This is time to add one more variable. Add weight to the model: This is pretty simple. In the model ‘m’, we considered only one explanatory variable ‘Age’. This time we will have two explanatory variables: Age and Weight. It can be done using the same ‘lm’ function and I will save this model in a variable ‘m1’. A very simple test known as the VIF test is used to assess multicollinearity in our regression model. The variance inflation factor (VIF) identifies the strength of correlation among the predictors. . We can directly use these standardized variables in our model. The advantage of standardizing the variables is that the coefficients continue .The goal of a multilinear regression model is to test if the variability in the independent variables (X's) can explain the variability in the dependent variable (Y). Select one: There are 3 steps to solve this one.Often times a statistical analyst is handed a set dataset and asked to fit a model using a technique such as linear regression. Very frequently the dataset is accompanied with a disclaimer similar to "Oh yeah, we messed up collecting some of these data points -- .
Note that in this case, the test data is 30% of the original data set as specified with the parameter test_size = 0.3. We have now created our training data and test data for our logistic regression model. We will train our model in the next .
Understand that the t-test for a slope parameter tests the marginal significance of the predictor after adjusting for the other predictors in the model (as can be justified by the equivalence of the t-test and the corresponding general linear F-test for . This is time to add one more variable. Add weight to the model: This is pretty simple. In the model ‘m’, we considered only one explanatory variable ‘Age’. This time we will have two explanatory variables: Age and .In statistics, multicollinearity or collinearity is a situation where the predictors in a regression model are linearly dependent.. Perfect multicollinearity refers to a situation where the predictive variables have an exact linear relationship. When there is perfect collinearity, the design matrix has less than full rank, and therefore the moment matrix cannot be inverted.
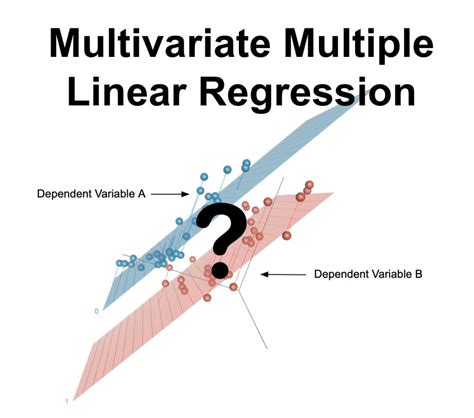
We would like to show you a description here but the site won’t allow us. The multi-target multilinear regression model is a type of machine learning model that takes single or multiple features as input to make multiple predictions. In our earlier post, we discussed how to make simple predictions with multilinear regression and generate multiple outputs. Here we’ll build our model and train it on a dataset. In this post, we’ll generate a .
Each of the predictor variables appears to have a noticeable linear correlation with the response variable mpg, so we’ll proceed to fit the linear regression model to the data. Fitting the Model The basic syntax to fit a multiple linear regression model in R is as follows:
Therefore, if the coefficients of variables are not individually significant – cannot be rejected in the t-test, respectively – but can jointly explain the variance of the dependent variable with rejection in the F-test and a high coefficient of determination (R 2), multicollinearity might exist. It is one of the methods to detect .
#1 Importing the libraries import numpy as np import pandas as pd import matplotlib.pyplot as plt #2 Importing the dataset: dataset = pd.read_csv(“50_Startups.csv”) #Y: dependent variable .
The goal of a multilinear regression model is to test if the variability in the independent variables (X's) can explain the variability in the dependent variable (Y). Select one: 1. Yes • 2. No. There are 2 steps to solve this one. Who are the experts? A related question that I have is that there are cases when I want to drop variables from the model (e.g. variable 73 out of 115) for a particular model run, but I don't want to cut vector #73 from the matrix because that would then make the estimated regression coefficients shift, e.g. regression coefficient for vector 74 would now become . And to select the features, we simply do like this: X_train _t = sel.transform(X_train) X_test _t = sel.transform(X_test). Simple! Considerations and Caveats. It’s crucial to note that the importance derived from permutation feature importance is relative to the model’s performance.A poorly performing model may assign low importance to a feature, while a well-performing .
where X is a n (p+1) matrix of random variables (including an all-and-always 1 rst column), and is an n 1 matrix of noise variables. By the modeling assumptions, E[ jX] = 0 while Var[ jX] = ˙2I. 2.2 The Statistical Model, Assuming Gaussian Noise In the multiple linear regression model with Gaussian noise,
webA Sim Empréstimos faz parte Grupo Santander e foi criada para facilitar e desburocratizar o acesso ao crédito. Por esse motivo, todo o processo de simulação, análise de crédito e contratação do empréstimo acontece 100% online. Esse modelo de negócio fez com que a Sim conquistasse milhões de clientes no país em busca de crédito para quitar dívidas, .
dropping variables from multilinear model test|when to drop variables in multiple linear regression